Leyes de los exponentes y radicales (con ejemplos resueltos)

En matemáticas, elevar un número a otro es lo que se conoce como una potencia, donde uno es la base y el otro es el exponente. Entonces, una potencia es el resultado de elevar la base a un exponente. En otras palabras, una potencia es el resultado de multiplicar un número por sí mismo tantas veces como diga el exponente.

Los radicales o raíces son las operaciones contrarias a las potencias, es decir, que son la cantidad de veces que multiplicas un número por sí mismo para obtener otro. Existen leyes que regulan la realización de las operaciones matemáticas tanto de exponentes como de radicales y las mismas, se enumeran a continuación.

Exponentes

Los exponentes son números que señalan la cantidad de veces que se va a multiplicar la base por ella misma en una operación con potencias.

Leyes de los Exponentes

Las leyes de los exponentes son las reglas que deben respetarse cuando se realizan operaciones con potencias. Ese número es conocido como la base y la cantidad de veces que se multiplica el número por sí mismo es el exponente.

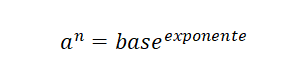
En esta expresión se indica la base y el exponente.

A continuación se presentan las leyes de los exponentes que rigen las operaciones con potencias:

Potencia con exponente cero y base diferente de cero

Cuando se tiene una potencia con exponente cero, cuya base es diferente de cero, el resultado es igual a uno.

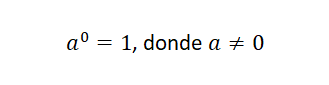
Como ejemplos tenemos:

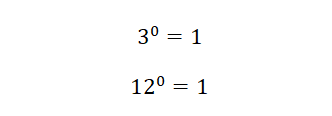
Potencia con exponente igual a uno

Cualquier potencia cuya base tiene un exponente igual a uno, da como resultado el número que es la base de la potencia.

Algunos ejemplos son:

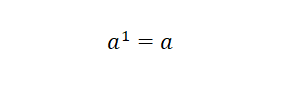
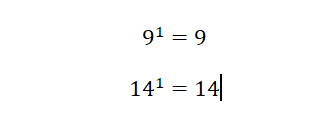
Producto de potencias de igual base

Para calcular un producto de potencias de igual base, se coloca la base y se suman los exponentes.

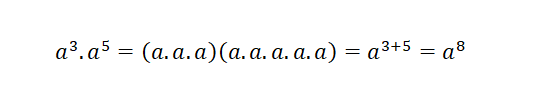
Unos ejemplos son:

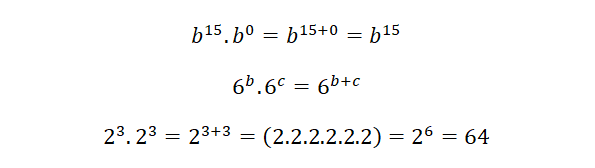
División de potencias de igual base

Cuando se necesita hacer una división de potencias de igual base, se obtiene la misma base y se restan los exponentes:

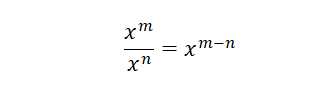
Como un ejemplo tenemos:

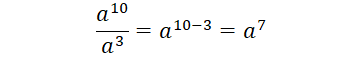
Cuando al restar los exponentes se obtiene un número negativo, se cumple que, todo número con exponente negativo es igual a su número inverso con exponente positivo.

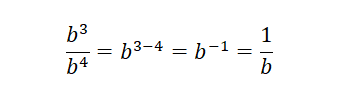
Otra manera de ver la división de potencias de igual base es eliminando los términos comunes que existen entre el numerador y el denominador, así:

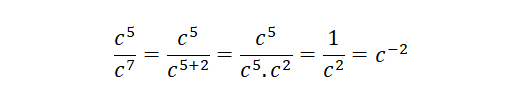
Potencia de un producto

Dado que una potencia no es otra cosa que multiplicaciones sucesivas, para la potencia de un producto también se cumple la propiedad distributiva. Esta propiedad establece que un producto elevado a la enésima potencia es igual a la multiplicación de cada uno de los factores elevado a esa misma potencia.

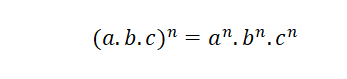
Unos ejemplos serían:

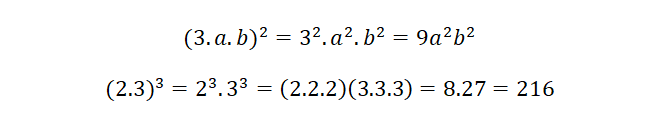
Potencia de una fracción

Para calcular la potencia de una fracción, se aplica la propiedad distributiva de la división exacta. Entonces, para elevar una fracción a una potencia, se elevan tanto el numerador como el denominador a la potencia, de la siguiente manera:

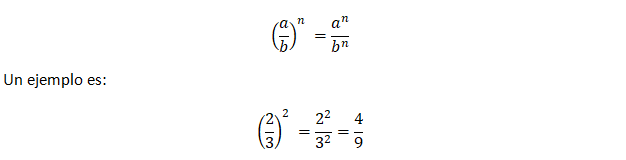
Potencia de una potencia

Una potencia de una potencia se realiza colocando la misma base y multiplicando los exponentes, es decir:

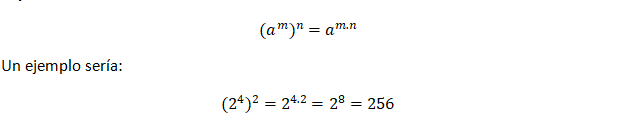
En otras palabras, si multiplicas potencias de igual base e igual exponente, el resultado es una potencia de otra potencia:

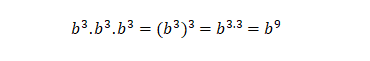
Radicales

Cuando realizas una operación contraria a una potencia, lo que obtienes es la raíz de un número o el radical. Es una operación que sirve para obtener la cantidad de veces que se requiere multiplicar un número b para tener como resultado un número a.

Esta cantidad de veces es el índice de la raíz, la cual indica el número de veces que se realiza la multiplicación. Para esta operación se utiliza un símbolo que se llama radical, un ejemplo que muestra que la raíz enésima de a es b , es la siguiente:

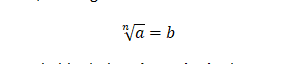
Cuando  es igual a dos, se habla de la raíz cuadrada de un número, por lo que la raíz cuadrada de a es b:

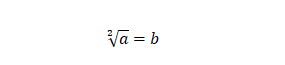
Normalmente, se escribe sin colocar el exponente, sobreentendiéndose que se trata de una raíz cuadrada.

√a=b

En otras palabras, la raíz cuadrada de dieciséis es cuatro, donde dos es la cantidad de veces que se multiplica cuatro por el mismo para obtener dieciséis:

√16=4

Leyes de los Radicales

Ahora que ya conoces la raíz de número, es importante que también conozcas las leyes de los radicales o raíces:

Raíz enésima de una potencia enésima

Si calculas la raíz enésima de un número elevado a la enésima potencia, el resultado será la base de la potencia, es decir:

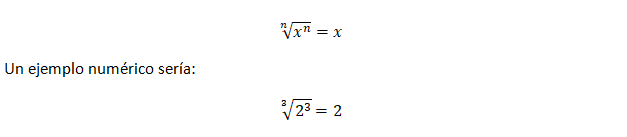
El exponente fraccionario

Raíz de una fracción

Al calcular la raíz de una fracción se obtiene como resultado la raíz del numerador dividida entre la raíz del denominador.

Raíz de una raíz

La raíz de una raíz se resuelve multiplicando los índices de ambas raíces, cuyo producto sería el nuevo índice de la nueva raíz.

Esta operación se ilustra así:

Raíz de un producto

Al calcular la raíz de un producto, se obtiene como resultado el producto de las raíces de los términos de la multiplicación.

Descubre también aquí la Ley de Ohm.