En matemáticas, la jerarquía de operaciones hace referencia al orden en que se deben ejecutar las operaciones matemáticas. Porque, la jerarquía de operaciones es un método para resolver operaciones matemáticas con varios signos de agrupación y múltiples operadores matemáticos.
Se llaman operadores matemáticos a los símbolos que nos permiten reconocer cual es la operación matemática que debemos realizar:
- Para la suma, el operador matemático es: “+”
- Para la resta, el operador matemático es: “-”
- Para la multiplicación, el operador matemático es: “.” o “×”
- Para la división, el operador matemático es: “÷” o “/”
Esta jerarquía establece por donde se debe iniciar la resolución de las operaciones, atendiendo las prioridades que se estipulan, tanto para los signos de agrupación como para los operadores matemáticos. En consecuencia, para resolver operaciones matemáticas hay que conocer dos cosas fundamentalmente:
- ¿Cómo suprimir los signos de agrupación?
- ¿Cuáles operadores tienen la mayor prioridad para iniciar a resolver las operaciones matemáticas?
Las reglas que rigen las respuestas a estas dos interrogantes, se conocen como la jerarquía de operaciones.
Contenido
Jerarquía de operaciones
La jerarquía de operaciones define, primero que todo, cuales son las prioridades de las operaciones matemáticas al momento de su ejecución. Y también define, cuales son las prioridades para suprimir los signos de agrupación.
Esas prioridades establecen tanto el orden en que deben realizarse las operaciones matemáticas como el orden en que deben eliminarse los signos de agrupación. Y de acuerdo con esas prioridades y el orden en que se ejecutan, se establecen las reglas que rigen la resolución de las operaciones matemáticas.
Signos de agrupación
Los signos de agrupación, como su nombre lo indica, sirven para señalar cuales son las operaciones que deben realizarse primero. Para hacer este señalamiento, se incluyen dentro de los signos de agrupación, las operaciones que catalogamos como prioritarias.
En matemática, los signos de agrupación más utilizados son:
- Los paréntesis ( )
- Los corchetes [ ]
- Las llaves { }
Adicionalmente, también se consideran signos de agrupación:
- Las barras de fracciones /
- Las barras que indican valor absoluto | |
- El símbolo de raíz √
Eliminación de los signos de agrupación
La eliminación de los signos de agrupación debe hacerse considerando las siguientes premisas:
- Si el signo de agrupación va precedido por un “+”, solo se elimina el signo de agrupación permitiendo que todos los términos internos conserven su signo, sea positivo o negativo.
- Si el signo de agrupación va precedido por un “-”, para eliminar el signo de agrupación se aplica la ley de los signos a todos y cada uno de los términos contenidos.
- El orden para la supresión de los signos de agrupación es primero los paréntesis, luego los corchetes y por último, las llaves.
Es importante destacar que, para cambiar los signos de cada término, debe respetarse también, la ley de los signos de la suma, resta, multiplicación y división.
Ejemplos de eliminación de los signos de agrupación
Considerando las premisas previamente expuestas, veamos cómo podemos aplicarlas en algunos ejemplos:
Ejemplo 1:
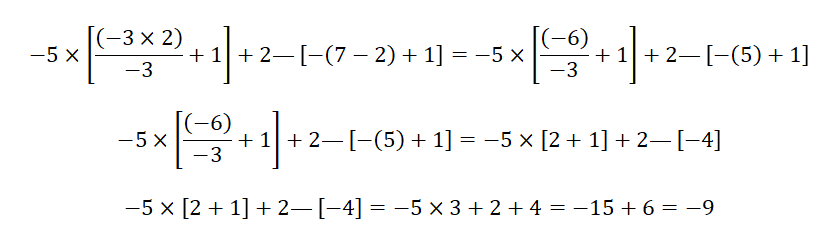
Ejemplo 2:
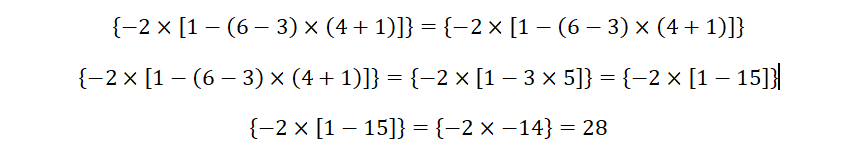
Reglas
Las reglas establecen el orden en que deben ejecutarse las operaciones dentro de una expresión numérica que contiene múltiples operaciones. El orden establecido para la resolución de las operaciones matemáticas es el siguiente:
Orden de los cálculos
Los cálculos de operadores con igual prioridad se realizan de izquierda a derecha.
Ejemplo 1:
4+115-9+10=119-9+10=110+10=120
Ejemplo 2:
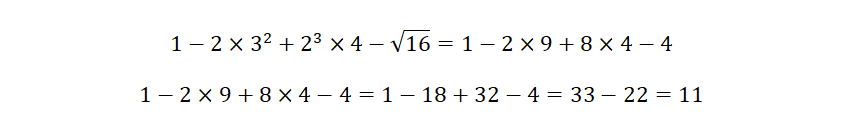
Eliminar signos de agrupación
Primero, se eliminan los signos de agrupación, realizando primero las operaciones contenidas en ellos.
Ejemplo 1:
(4+115)-(9-10)=119-(-1)=119+1=120
Ejemplo 2:
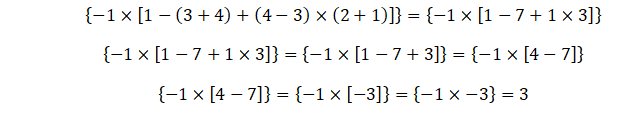
Resolver exponentes y radicales
Seguidamente, se resuelven los exponentes o potencias y los radicales o raíces.
Como en este ejemplo:
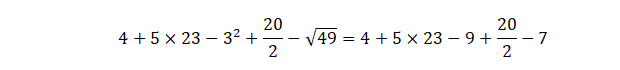
Resolver multiplicaciones y divisiones
El próximo paso es resolver las multiplicaciones y divisiones.
Veamos este ejemplo:
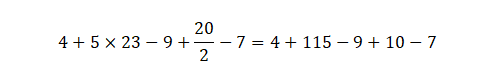
Resolver sumas y restas
Como último paso, se agrupan los números positivos y los negativos, antes de resolver las sumas y/o las restas.
4+115-9+10-7=129-16=113
Prioridad en la resolución de operaciones matemáticas
Es importante establecer cuál es la prioridad en la resolución de operaciones matemáticas que debes considerar para obtener un resultado correcto:
Paso 1
Cuando no hay signos de agrupación, se comienza resolviendo los exponentes, luego las multiplicaciones y divisiones, después se agrupan los números positivos y negativos, antes de sumarlos o restarlos.
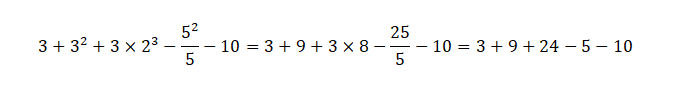
3+9+24-5-10=36-15=21
Paso 2
Si hay signos de agrupación, se calculan las expresiones dentro de los signos de agrupación, antes de eliminarlos usando la ley de los signos, para después ejecutar el paso 1.
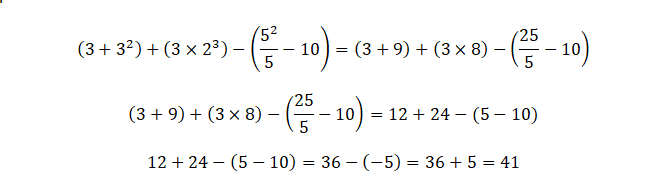
En resumen
En las operaciones matemáticas, hay niveles que no se pueden mezclar al resolverlas y siempre se debe iniciar a partir de las más complejas, como los exponentes y radicales. Continuando hasta alcanzar los niveles más simples, como las sumas y las restas.
Igualmente, es fundamental saber que si existen signos de agrupación, ya sean paréntesis, corchetes y/o llaves, primero hay que resolver las operaciones que están dentro de ellos. Y en todos los momentos, mientras se resuelven las operaciones hay que respetar las leyes de los signos de la suma, resta, multiplicación y división.
Ejercicios resueltos
A continuación, se presentan algunos ejercicios resueltos que ilustran lo visto hasta ahora en relación con la jerarquía de operaciones:
Ejercicio 1
Comenzando, se realizan las operaciones que están dentro de los paréntesis:
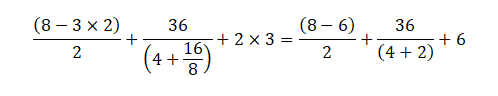
Una vez hechos estos cálculos, se procede a eliminar los paréntesis:
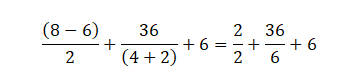
Ahora, se resuelven las divisiones:
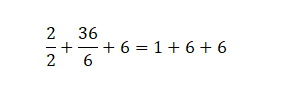
Finalmente, se resuelven las sumas:
1+6+6=13
Ejercicio 2
Iniciando, se resuelven las operaciones que están dentro de los paréntesis:
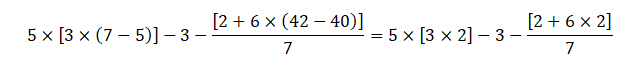
Segundo, se resuelven las operaciones matemáticas que están dentro de los corchetes:
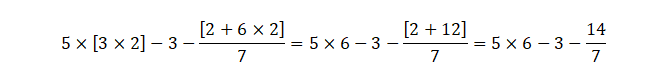
Tercero, se resuelven las multiplicaciones y divisiones:
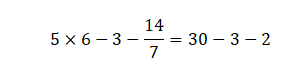
Cuarto, se resuelven las sumas y restas, agrupando los números positivos y negativos:
30-3-2=30-5=25


Hay veces que el símbolo de multiplicar no se escribe y queda de forma omitida como en 8:2(2+2).
En este caso, ?esta expresión equivale a
8:2*(2+2) o por el contrario equivale a
8:(2*(2+2)?
En caso de que sea la primera opción, ?por qué la expresión 8:2X equivale a 8:(2*X) y no a 8:2*X?
Resolver este ejercicio: 7 x 8 : 7 x 8 = ?
Para este ejercicio: 7 x 8 : 7 x 8 :
1)Empezamos de izquierda a derecha y siguiendo el <>.
¡IMPORTANTE!:
QUE ENTIENDAS EL TEMA JERARQUÍA DE LAS OPERACIONES:TE DEJO UN LINK PARA QUE LO REPASES:https://www.youtube.com/watch?v=XV5PiV2-91U
También que sepas multiplicar y dividir,que para eso tienes que saber ,sumar,restar.Qee para eso debes entender el porque usamos los números.
1)empezamos por los parentésis,pero como no tiene paréntesis pasamos a lo siguiente .
2)raíces y potencias,vemos que no hay raíces ni potencias ,entonces pasamos a lo siguiente.
3)multiplicación y división,en este caso si hay.
<>.
en este caso hay una multiplicación,debes de entender que cuando hay una multiplicación se cuenta como un solo número es decir (7 x 8) es un solo número ten lo en cuenta ,entonces solucionamos la multiplicación primero porque empezamos de izquierda a derecha y la primera operación de izquierda a derecha es una multiplicación,es decir,empezamos por la multiplicación.
7 x 8 : 7 x 8 ; resolviendo la multiplicación quedaría lo siguiente:
56 : 7 x 8 ,ahora nos quedaría el otro número ,que en este proceso no debemos confundir que 56 : 7 es un número ,debido a que primero hacemos las multiplicaciones y después las divisiones ya que empezamos de izquierda a derecha y había una multiplicación de primeritas entonces hacemos todas las multiplicaciones ,en este caso tenemos 7 x 8 tendriamos 56,Ahora tendríamos lo siguiente 56 : 56 ,ahora nos quedaría una división efecutamos la división.Quedando 56 : 56 =1 ,es decir que nos dio como resultado la unidad o uno.Ese sería el resultado de esta operación.
¿Quién sabe resolver este ejercicio? 7 x 3 : 7 x 3 = ?
Es 21
NO SE COMO RESOLVER ESTA OPERACION
4-{-5-9-[-(-5·-4+6:-3)-9·-30:-6+7]-3 }-3:-3
Primero resolvemos el paréntesis, para ello, realizo el producto, y el cociente por separado, sumo los resultados de ese producto y cociente. Al resultado del paréntesis, le cambiamos el signo (por el signo menos que hay delante.
Ya en el corchete, resuelvo el producto -9 por -30, lo que de lo dividimos entre -6 y por último hago las sumas y restas que me quedan. Como el corchete va precedido de signo menos, cambio el signo del resultado.
Dentro de la llave, sólo quedan sumas o restas, las resolvemos para eliminar la llave y dejar el valor resultante. Como también está precedida de signo menos, cambiamos el signo del resultado.
Eliminada la llave, realizamos primero el cociente -3 entre -3 y ese +1 se opera con el resultado de la llave y el 4 que teníamos en primer lugar…… EL RESULTADO DEBE DAR 6
Oye no sería 319?
526378382818
Empieza del centro hacia afuera, resolviendo por jerarquía de operadores (multiplicación y división primero, después la suma o resta).
Después, resuelves el paréntesis del centro, y eliminas el paréntesis al multiplicar por el signo que esta a la izquierda, a un lado del paréntesis (del centro hacia afuera).
Nota: Los “:“ es division
No se puede escribir -5 . -3 , ni 30 : -6 Después de la multiplicación o división, si es con un número negativo, este, ha de estar entre paréntesis.
muy buenos ejercicios!! en verdad me sirvieron