En matemáticas, los números reales son un conjunto que incluye a los números naturales, los enteros, los racionales y los irracionales. Es decir, que los números reales abarcan la mayoría de los números que usamos en nuestro día a día. Este conjunto de los números reales se identifica con la letra R.
La palabra real se utiliza para distinguir a los números reales de los números imaginarios, identificados con la letra i. Donde i es igual a la raíz cuadrada de -1, en otras palabras:
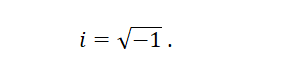
Lo realmente interesante de conocer los diferentes tipos de números es que ayudan a incrementar el razonamiento abstracto.
Contenido
Números reales
Los números reales incluyen tanto a los números positivos como a los negativos, el número cero y los números que no se pueden escribir usando fracciones de dos enteros. Todos los números reales tienen un orden y se escriben en forma de un número decimal.
Un número real está compuesto de un número entero, un decimal exacto, un decimal periódico o un decimal con infinitas cifras no periódicas.
Clasificación de los números reales
La clasificación de los números reales establece la existencia de los números naturales, los números enteros, los números racionales y los números irracionales. A continuación mostramos esta clasificación:
Números naturales
Los números naturales son el conjunto de los números que se usan para contar y que no tienen una parte decimal o fracción. Este conjunto de los números naturales está representado por la letra N y está formado por los números: {0,1,2,3,4…}
Algunos ejemplos del uso de los números naturales son los siguientes:
- Hay doce rosas en el jardín.
- La población de Suiza es de ocho millones de personas.
- La suma de tres más tres es seis.
Es importante destacar, que algunas clasificaciones definen al número cero como un número natural, mientras que otras no lo hacen así.
Los números naturales son las bases con la que se construyen muchos de los otros conjuntos de números, como los enteros, racionales, reales y complejos, inclusive. Debido a su importancia, la teoría de números estudia las propiedades de los números naturales, como la divisibilidad y la distribución de los números primarios. Por otro lado, la combinatoria estudia los problemas relacionados con contar y ordenar, como las enumeraciones y la partición.
Números enteros
Los números enteros son el conjunto de los números naturales más sus contrarios, sin considerar los números que tienen una parte decimal. Este conjunto de los números enteros está representado por la letra Z y está formado por los números: {0,1,-1,2,-2,3,-3,4…}
Algunos ejemplos del uso de los números enteros son los siguientes:
- La temperatura más baja en la que he estado en invierno es -10 grados.
- Me gradué de la secundaria hace 20 años.
- Mi primo quedó de 3° lugar en la competencia de atletismo.
En cambio, no son números enteros aquellos que tienen un componente fraccional, como por ejemplo: 9,75 o √3. El conjunto Z de los números enteros es un grupo contable e infinito, que a su vez, es un subconjunto de los números racionales, los que veremos a continuación.
Números racionales
Los números racionales son el conjunto de los números naturales más sus opuestos, incluyendo los números que tienen una parte decimal. En otras palabras, los números racionales son los números que están compuestos de fracciones de números enteros.
Este conjunto de los números racionales está representado por la letra Q e incluye los números enteros y cualquier otro número que sea el resultado de una fracción.
El conjunto Q de los números racionales es un grupo infinito, pero no es contable, ya que todas las fracciones forman parte de él.
Debido a que el resultado de una fracción puede ser un número entero, ello significa que los números enteros también pueden ser considerados como números racionales. En otras palabras, el conjunto Z de los números enteros está incluido dentro del conjunto Q de los números racionales. Entonces, este conjunto Q incluye a los números naturales, a los números enteros, a los números decimales exactos y a los números decimales inexactos.
La expansión decimal de un número racional puede terminar en:
- Una cantidad finita de dígitos o número decimal exacto, como 14,50.
- Una secuencia repetida de un dígito o número decimal inexacto, como 0,34566666666…
Debido a esto, dentro de los números racionales se incluyen los números periódicos puros o números periódicos mixtos.
Números irracionales
Los números irracionales son el conjunto de los números que tienen una parte decimal, que no puede escribirse como el resultado de dividir números enteros. Este conjunto de los números irracionales está representado por la letra e incluye los números cuyas cifras decimales son interminables e irrepetibles.
Un ejemplo de un número irracional es el número π (pi) cuyo valor es aproximadamente: 3,14159265358979.
Es decir, que un número irracional tiene infinitos decimales, que no son periódicos. Entonces, los radicales o raíces que no pueden expresarse a través de ningún número entero, ni fracción, también son números irracionales.
El conjunto I de los números irracionales es un grupo infinito, que no es contable. El conjunto I de los números irracionales se escribe como el conjunto R de los números reales menos el conjunto Q de los números racionales, es decir que: I=R-Q.
Entonces, los números irracionales son todos aquellos números reales que no incluyen a los racionales.
Propiedades de los números reales
Las propiedades de los números reales están resumidas en las reglas que se exponen a continuación:
Propiedad conmutativa
La suma de números reales cumple con la propiedad conmutativa, es decir, que la posición de las variables no altera el resultado:
a+b=b+a
La multiplicación de números reales cumple con la propiedad conmutativa, es decir, que la posición de las variables no altera el producto:
a.b=b.a
Propiedad asociativa
La suma de números reales cumple con la propiedad asociativa, es decir:
(a+b)+c=a+(b+c)
La multiplicación de números reales cumple con la propiedad asociativa, es decir:
(a.b).c=a.(b.c)
Elemento neutro
En el caso de la suma de números reales, se cumple que el cero es el elemento neutro de la suma.
Por lo que, cuando se suma cualquier número real a más cero, el resultado es el mismo número real, es decir:
a+0=a
En el caso de la multiplicación de números reales, se cumple que el uno es el elemento neutro de la multiplicación.
Por lo que, cuando se multiplica cualquier número real a por uno, el resultado es el mismo número real, o sea que:
a.1=a
Operaciones cerradas
El resultado de las operaciones de suma y/o multiplicación de números reales también es un número real.
Elemento simétrico o inverso aditivo
En la suma de números reales se cumple que para número real existe otro número real que es su elemento simétrico, porque uno sumado con el otro, da como resultado cero.
a+(-a)=0
Inverso multiplicativo
En la multiplicación de números reales se cumple que todo número real tiene otro número real que es su inverso multiplicativo, porque uno multiplicado con el otro, da como resultado uno.
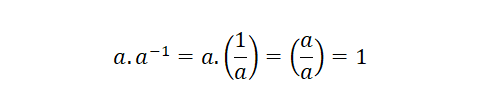
Propiedad distributiva de la multiplicación
La suma y multiplicación de números reales cumple con la propiedad distributiva, es decir:
a.(b+c)=(a.b)+(a.c)


Me pareció muy interesante el tema porque me dió información muy interesante.
Me explico los diferentes tipos de números como naturales, enteros y de como se hacen algunos procedimientos para sabe el resultado de alguna superación.