Las integrales son un concepto fundamental en el cálculo, una rama de las matemáticas que permite estudiar cambios, áreas, volúmenes y muchas otras propiedades. Para quienes recién comienzan, comprender las integrales puede parecer un desafío, pero con una explicación clara y un enfoque paso a paso, su utilidad y lógica se vuelven evidentes.
Contenido
¿Qué son las integrales?
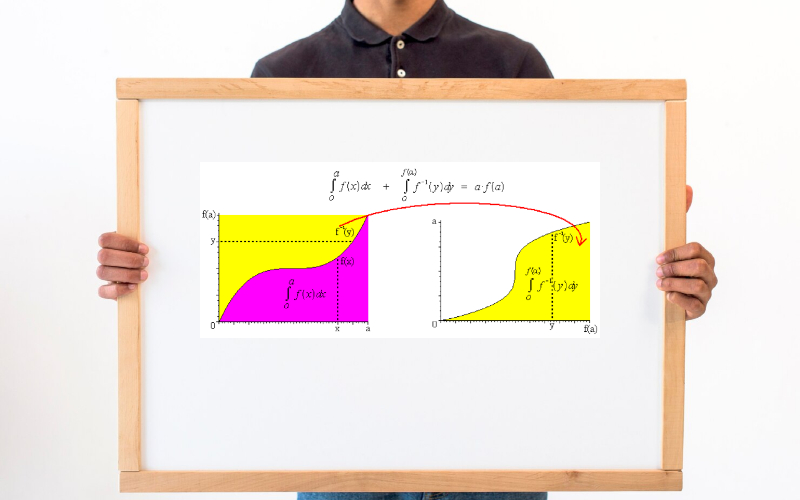
En términos simples, una integral puede considerarse como una herramienta matemática que ayuda a calcular el área bajo una curva. Mientras que la derivada analiza cómo cambian las funciones, la integral se ocupa de acumular esos cambios. En otras palabras, si la derivada responde a «¿qué tan rápido cambia algo?», la integral responde a «¿cuánto se acumula?».
Hay dos tipos principales de integrales:
- Integral definida: Calcula un valor numérico, representando el área bajo una curva en un intervalo específico.
- Integral indefinida: Representa una familia de funciones cuya derivada es la función dada.
Ambas tienen aplicaciones prácticas importantes en diversas áreas, desde la física hasta la economía.
Conceptos básicos antes de comenzar
Para comprender mejor las integrales, es útil repasar algunos conceptos clave:
- Funciones: Una función es una relación que asocia cada valor de entrada con un valor de salida. Por ejemplo, y=x2y = x^2y=x2 es una función cuadrática.
- Áreas bajo curvas: Cuando graficamos una función, podemos visualizar el área entre la curva y el eje x. Las integrales nos permiten calcular este valor, incluso si la forma no es un rectángulo o un triángulo.
- Límites: Las integrales se apoyan en el concepto de límites, donde se divide el área en pequeñas secciones y luego se suman infinitesimalmente.
Con estas nociones básicas en mente, el siguiente paso es profundizar en cómo se construyen las integrales.
Integral definida: una mirada inicial
La integral definida tiene una notación característica:
∫abf(x) dx\int_a^b f(x) \, dx∫abf(x)dx
Cada elemento de esta notación tiene un significado importante:
- f(x)f(x)f(x): Es la función que estamos integrando.
- aaa y bbb: Representan los límites inferior y superior, respectivamente. Estos indican el intervalo en el que calcularemos el área.
- dxdxdx: Indica que estamos integrando con respecto a la variable xxx.
Un ejemplo sencillo ayuda a ilustrar este concepto. Supongamos que queremos calcular el área bajo la función f(x)=xf(x) = xf(x)=x entre x=0x = 0x=0 y x=2x = 2x=2. Esto se representa como:
∫02x dx\int_0^2 x \, dx∫02xdx
La solución implica encontrar la antiderivada de f(x)f(x)f(x), que es x22\frac{x^2}{2}2×2, y luego evaluarla en los límites dados:
[x22]02=222−022=2\left[ \frac{x^2}{2} \right]_0^2 = \frac{2^2}{2} – \frac{0^2}{2} = 2[2×2]02=222−202=2
El resultado, 2, representa el área bajo la curva entre los puntos especificados.
Integral indefinida: una visión general
A diferencia de la integral definida, la integral indefinida no tiene límites. Su notación es más simple:
∫f(x) dx\int f(x) \, dx∫f(x)dx
El objetivo principal es encontrar la función F(x)F(x)F(x) cuya derivada sea f(x)f(x)f(x). Esto se conoce como la antiderivada de f(x)f(x)f(x). Un detalle importante es que las integrales indefinidas incluyen una constante de integración (CCC), porque múltiples funciones pueden tener la misma derivada.
Por ejemplo, si f(x)=2xf(x) = 2xf(x)=2x, su integral indefinida es:
∫2x dx=x2+C\int 2x \, dx = x^2 + C∫2xdx=x2+C
Esto se debe a que la derivada de x2+Cx^2 + Cx2+C siempre será 2x2x2x, independientemente del valor de CCC.
Regla fundamental del cálculo
La regla fundamental del cálculo conecta las derivadas y las integrales, proporcionando una base teórica sólida. Esta regla tiene dos partes principales:
- Primera parte: Si F(x)F(x)F(x) es una antiderivada de f(x)f(x)f(x), entonces la integral definida de f(x)f(x)f(x) desde aaa hasta bbb se calcula como:
∫abf(x) dx=F(b)−F(a)\int_a^b f(x) \, dx = F(b) – F(a)∫abf(x)dx=F(b)−F(a)
- Segunda parte: La derivada de la integral acumulativa de una función f(x)f(x)f(x) es igual a f(x)f(x)f(x). En notación:
ddx(∫axf(t) dt)=f(x)\frac{d}{dx} \left( \int_a^x f(t) \, dt \right) = f(x)dxd(∫axf(t)dt)=f(x)
Esta conexión destaca cómo las integrales y las derivadas son operaciones inversas entre sí.
Métodos básicos para resolver integrales
Existen diversas técnicas para calcular integrales, y algunas son más comunes en los niveles iniciales:
Regla de potencia
Para funciones en la forma xnx^nxn, la integral se calcula utilizando la regla de potencia:
∫xn dx=xn+1n+1+C(para n≠−1)\int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad \text{(para \( n \neq -1 \))}∫xndx=n+1xn+1+C(para n=−1)
Por ejemplo:
∫x3 dx=x44+C\int x^3 \, dx = \frac{x^4}{4} + C∫x3dx=4×4+C
Descomposición en sumas
Si una función es la suma de varias partes, se puede integrar cada término por separado. Por ejemplo:
∫(3×2+2x+1) dx=∫3×2 dx+∫2x dx+∫1 dx\int (3x^2 + 2x + 1) \, dx = \int 3x^2 \, dx + \int 2x \, dx + \int 1 \, dx∫(3×2+2x+1)dx=∫3x2dx+∫2xdx+∫1dx
Resolviendo cada término, obtenemos:
x3+x2+x+Cx^3 + x^2 + x + Cx3+x2+x+C
Uso de constantes
Cuando una constante multiplica a una función, puede sacarse fuera del signo de integral:
∫k⋅f(x) dx=k∫f(x) dx\int k \cdot f(x) \, dx = k \int f(x) \, dx∫k⋅f(x)dx=k∫f(x)dx
Por ejemplo:
∫5x dx=5∫x dx=5⋅x22+C=5×22+C\int 5x \, dx = 5 \int x \, dx = 5 \cdot \frac{x^2}{2} + C = \frac{5x^2}{2} + C∫5xdx=5∫xdx=5⋅2×2+C=25×2+C
Aplicaciones de las integrales
Las integrales tienen un impacto significativo en diversas áreas de la ciencia y la ingeniería. Algunas aplicaciones comunes incluyen:
- Cálculo de áreas: Determinar áreas bajo curvas o entre funciones.
- Volúmenes: Calcular volúmenes de sólidos de revolución mediante métodos como el disco o la arandela.
- Física: Hallar desplazamientos, velocidades y energías acumulativas.
- Economía: Modelar ingresos totales o costos acumulados.
Estas aplicaciones ilustran cómo las integrales trascienden el ámbito matemático y se convierten en herramientas prácticas para resolver problemas del mundo real.
Consejos para principiantes
Para quienes inician su estudio de las integrales, estos consejos pueden ser útiles:
- Domina las derivadas: Comprender las derivadas facilita el aprendizaje de las antiderivadas.
- Practica con ejemplos básicos: Resolver problemas sencillos construye confianza antes de abordar casos más complejos.
- Memoriza fórmulas clave: Tener presente las reglas básicas de integración agiliza los cálculos.
- Consulta gráficos: Visualizar las funciones y las áreas puede aclarar conceptos abstractos.
Reflexión final
Las integrales son una herramienta poderosa que permite comprender y resolver problemas relacionados con la acumulación y el cambio. Aunque su aprendizaje inicial requiere paciencia y práctica, su utilidad en matemáticas y en el mundo real es invaluable. Con una base sólida en los conceptos fundamentales y un enfoque sistemático, cualquier estudiante puede dominar este fascinante tema.